標準得点、標準偏差とは
標準得点、標準偏差とは
ここでは標準得点について簡単に説明します。
検査の得点は、学校の試験のように100点満点で表されることも多いですが、同じ得点であっても問題の難易度によりその意味が異なってきます。例えば、国語と数学の試験で両方とも80点をとったAさんについて考えてみましょう。単純に考えると、Aさんの国語の能力と数学の能力は同レベルであるように思えます。しかし次のような条件ではどうでしょうか。
| 平均点 | Aさんの得点 | |
|---|---|---|
| 国語 | 50点 | 80点 |
| 数学 | 70点 | 80点 |
数学の平均点が70点であるのに対し、国語の平均点は50点となっています。この条件下では、Aさんの数学の能力は平均レベルよりやや上ですが、国語の能力は平均よりもかなり高いと考えられます。
それでは、平均点がわかればよいのでしょうか。下のような条件では、Aさんの能力はどちらが高いと考えられるでしょうか。
| 平均点 | 値のばらつき | Aさんの得点 | |
|---|---|---|---|
| 国語 | 50点 | 大きい(高得点者と低得点者の差が大きい) | 80点 |
| 数学 | 70点 | 小さい(ほとんどの人が平均得点である) | 80点 |
国語では満点の人が多く、極端に点数が低い人もいたため平均点が50点となっています。一方数学では、ほとんどの人が平均得点である70点前後の得点で80点をとる人は少ない状況でした。この場合、Aさんは国語よりも数学の能力が高いと考えられます。
以上のように、同じ得点であっても平均点と分布の広がりの違いによって意味が異なってきます。したがって、検査の得点は平均点と分布状態の両方が明らかになってはじめて、比較したり評価したりできるのです。
普通に得点を求めた場合、各検査の平均点や分布の状態はバラバラであり、検査間で比較を行うことができません。そこで使用されるのが、標準化という手法です。統計学的な考え方にもとづき、平均点、分布のばらつきを一定の値にそろえます。SCOAでは平均点が50点、得点分布を一定の形(これを「正規分布」といいます)になるように変換した標準得点を使用しています。この標準得点を使えば、個人内の各検査(尺度)間の比較や、同一検査(尺度)についての個人間の比較・評価が客観的にできることになります。また、標準得点の50点は全国平均と対応していますから、標準得点によって個人のレベルの相対的な位置を把握することもできます。
総合得点の算出
基礎能力検査 総合得点について
一例として、SCOA総合適性検査は、尺度ごとに標準化された得点で表示されます。
そして、全体的な基礎能力の指標として、総合得点を算出し表示しています。総合評価は5つの能力について、単に合計するのではなく、能力の核となる部分と応用の部分にわけ、ウエイトをつけています。その値について、標準化を行い表示しています。これを標準得点の再標準化といいます。
再標準化の必要性
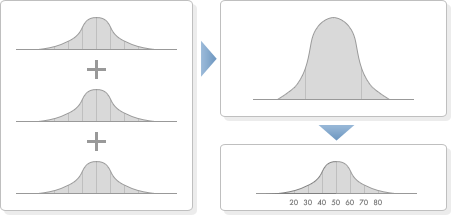
いくつかの標準得点を平均する場合、その値の分布は正規分布を示さず中心に集中する分布となります。SCOA総合適性検査の総合得点は、正規分布になるように再標準化をしています。したがって、個々の尺度の標準得点の平均が総合得点になっているわけではなく、総合得点が70点の場合は、個々の尺度と同様に、全国レベルで上位2~3%の位置にいる優れた能力であるといえます。
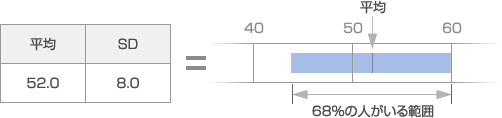
標準偏差(SD)
標準偏差(SD)とは、得点のばらつき(分布)を示す指標です。平均値をはさむ±1SDの間に約7割(68%)の人がいることを示しています。(以下の例では、52+8=60点から52-8=44点の間)
標準得点のSDは10点を基準としています。10点以下の場合は、得点分布が集中しているといえます。